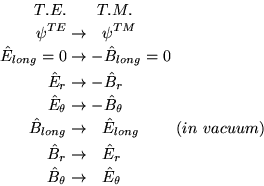Next: RADIATION: MATHEMATICAL RELATION TO
Up: Application to Accelerated and
Previous: The T.M. Field
There is a quick way of obtaining all the physical (orthonormal)
components of the electric and magnetic field. Note that the
longitudinal electric and magnetic field components 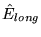 and
and
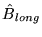 are scalars in the Lorentz plane and in the Euclidean
plane transverse to it. Consequently, for these components the
transition from Minkowski to Rindler/polar coordinates could have been
done without any computations. The same is true for the
two-dimensional transverse electric and magnetic field vectors. As
suggested by Eqs.(25) and
(26), in the denominator of the partial
derivatives simply make the replacements
are scalars in the Lorentz plane and in the Euclidean
plane transverse to it. Consequently, for these components the
transition from Minkowski to Rindler/polar coordinates could have been
done without any computations. The same is true for the
two-dimensional transverse electric and magnetic field vectors. As
suggested by Eqs.(25) and
(26), in the denominator of the partial
derivatives simply make the replacements
in Rindler sectors  or
or 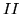 , and
, and
in Rindler sectors 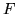 or
or 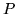 . These replacements yield the computed
transverse T.E. and T.M. components.
. These replacements yield the computed
transverse T.E. and T.M. components.
There also is a quick way of obtaining the T.M. field from the
T.E. field components. Let 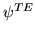 be the scalar wave function
which satisfies the Klein-Gordon wave function for the T.E. field,
and let
be the scalar wave function
which satisfies the Klein-Gordon wave function for the T.E. field,
and let 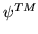 be that for the T.M. field. Then the corresponding
field components are related as follows:
be that for the T.M. field. Then the corresponding
field components are related as follows:
This relationship holds in all four Rindler sectors. It also holds
correspondingly relative to the rectilinear coordinate frame in
Sections IVA2 and IVA1.



Next: RADIATION: MATHEMATICAL RELATION TO
Up: Application to Accelerated and
Previous: The T.M. Field
Ulrich Gerlach
2001-10-09
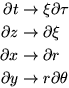
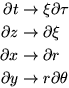
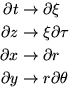
![]() be the scalar wave function
which satisfies the Klein-Gordon wave function for the T.E. field,
and let
be the scalar wave function
which satisfies the Klein-Gordon wave function for the T.E. field,
and let ![]() be that for the T.M. field. Then the corresponding
field components are related as follows:
be that for the T.M. field. Then the corresponding
field components are related as follows: