


Next: Flow of Radiant T.E.
Up: Axially Symmetric Source and
Previous: Magnetic Dipole and its
The most important electric dipole radiators are two linear antennas
each of length 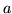 aligned parallel to the
aligned parallel to the 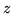 -axis, located at
-axis, located at
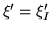 and
and
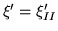 located in Rindler sectors
located in Rindler sectors  and
and 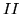 ,
and hence accelerated into opposite directions. Suppose each
antenna has electric dipole moment
,
and hence accelerated into opposite directions. Suppose each
antenna has electric dipole moment
Its charge-flux four-vector obtained from Eq.(31) is
and the corresponding scalar source function 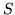 for Eq.(27) is
for Eq.(27) is
![\begin{displaymath}
S:\quad S_{I,II}(\tau',\xi',r',\theta')=
q_{I,II}(\tau')a~\...
...uad
\left[\frac{\textrm{charge}}{\textrm{length}^2} \right]~.
\end{displaymath}](img334.png) |
(63) |
This source is symmetric around the 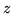 -axis because it is non-zero only at
-axis because it is non-zero only at 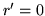 .
The electric dipole moment is the proper volume integral of this source,
.
The electric dipole moment is the proper volume integral of this source,
The axial symmetry of the source implies that its radiation is
independent of the polar angle 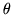 . Consequently, except some for a
source-dependent factor, the scalar field
. Consequently, except some for a
source-dependent factor, the scalar field 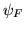 in
in 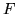 is the same
as Eq.(61).
One finds
is the same
as Eq.(61).
One finds
This is the T.M. scalar field due to a pair of localized linear
antennas, both situated on the 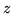 -axis, each one with its own
time-dependent dipole moment
-axis, each one with its own
time-dependent dipole moment 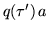 . By setting one of them to
zero one obtains the radiation field due to the other.
. By setting one of them to
zero one obtains the radiation field due to the other.



Next: Flow of Radiant T.E.
Up: Axially Symmetric Source and
Previous: Magnetic Dipole and its
Ulrich Gerlach
2001-10-09
![]() aligned parallel to the
aligned parallel to the ![]() -axis, located at
-axis, located at
![]() and
and
![]() located in Rindler sectors
located in Rindler sectors ![]() and
and ![]() ,
and hence accelerated into opposite directions. Suppose each
antenna has electric dipole moment
,
and hence accelerated into opposite directions. Suppose each
antenna has electric dipole moment
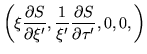
![$\displaystyle \left( q_{I,II}(\tau')a\frac{d}{d\xi'}\delta(\xi'-\xi'_{I,II}),
\...
...\theta'_0)}{r'}
~,\quad \left[\frac{\textrm{charge}}{\textrm{length}^3} \right]$](img333.png)