


Next: UNIFYING PERSPECTIVE
Up: RADIATION FROM VIOLENTLY ACCELERATED
Previous: VIOLENT ACCELERATION
Consider a dipole moment, m or d, which is
time-independent in its own accelerated frame. The augmented Larmor
formula, Eq.(70) and
(69), yields zero radiative
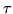 -momentum relative the expanding inertial frame in Rindler
sector
-momentum relative the expanding inertial frame in Rindler
sector 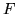 :
:
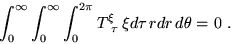 |
(73) |
However, for a non-zero static dipole moment the other
momenergy![[*]](footnote.png) components, also measured in
components, also measured in 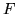 , are non-zero:
, are non-zero:
Equations (73)-(76) express an observationally and hence
conceptually precise distinction between the radiative and
non-radiative e.m. fields of a dipole source accelerated in Rindler
sector  : The augmented Larmor formula implies that the dipole emits
radiation if and only if its
: The augmented Larmor formula implies that the dipole emits
radiation if and only if its 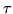 -momentum, the spatial integral of
-momentum, the spatial integral of
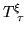 in the expanding inertial frame, is non-zero.
Furthermore, the existence of a dipole field, static in Rindler sector
in the expanding inertial frame, is non-zero.
Furthermore, the existence of a dipole field, static in Rindler sector
 , is expressed by the non-vanishing of the other momenergy
components, Eqs.(74)-(75). Like the
, is expressed by the non-vanishing of the other momenergy
components, Eqs.(74)-(75). Like the 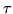 -momentum, these components are also
measurable in the expanding inertial frame. If the dipole is not
static then the the emitted radiation gets tracked by the
-momentum, these components are also
measurable in the expanding inertial frame. If the dipole is not
static then the the emitted radiation gets tracked by the
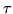 -momentum. In that case the other momenergy components play an
auxiliary role. They only track the sum of static dipole field and
the radiative field, not the separate contributions.
-momentum. In that case the other momenergy components play an
auxiliary role. They only track the sum of static dipole field and
the radiative field, not the separate contributions.



Next: UNIFYING PERSPECTIVE
Up: RADIATION FROM VIOLENTLY ACCELERATED
Previous: VIOLENT ACCELERATION
Ulrich Gerlach
2001-10-09
![]() -momentum relative the expanding inertial frame in Rindler
sector
-momentum relative the expanding inertial frame in Rindler
sector ![]() :
:
![[*]](footnote.png) components, also measured in
components, also measured in