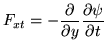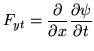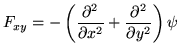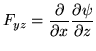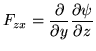

Next: The T.M. Field
Up: The Method of the
Previous: The Method of the
The T.E. Field
For the T.E. degrees of freedom the components of the charge-current
four-vector are
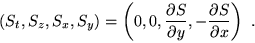 |
(9) |
The components of the T.E. vector potential are
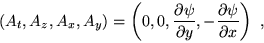 |
(10) |
and those of the e.m. field are
These components are guaranteed to satisfy all the Maxwell field equations
with T.E. source, Eq.(9), whenever 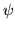 satisfies the inhomogeneous scalar wave equation, Eq.(5).
satisfies the inhomogeneous scalar wave equation, Eq.(5).
Ulrich Gerlach
2001-10-09