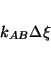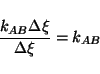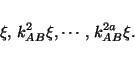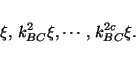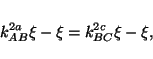


Next: Commensurable Accelerated Clocks
Up: Adjacent Clocks
Previous: Adjacent Clocks
Contents
Consider a pair of clocks AB and BC,
where all three radar units A, B, and C are freely floating, and radar
unit B is common to AB and BC, as in Fig. 5.
Figure 5:
Two adjacent geometrical
clocks consisting of inertially expanding cavities AB and BC, each
containing a pulse bouncing back and forth. Depicted in this diagram
are sequences of 2 pulses coming from A and impinging on B which are
matched by corresponding sequences of 3 pulses coming from C. The
ratio 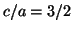 is the ticking rate of BC normalized to that of
AB. The fact that this ratio stays constant throughout the history
of the two clocks makes them commensurable.
is the ticking rate of BC normalized to that of
AB. The fact that this ratio stays constant throughout the history
of the two clocks makes them commensurable.
![\includegraphics[scale=.5]{two_inertial_clocks}](img73.png) |
What is the ratio 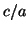 of two matched
pulse sequences impinging on radar unit B and coming from radar units
A and C? This ratio is determined by the following mini-calculation:
of two matched
pulse sequences impinging on radar unit B and coming from radar units
A and C? This ratio is determined by the following mini-calculation:
Let A emit two pulses separated by
as measured by atomic clock A. Due to the relative motion of A and B
these two pulses, once received at B, have time separation
as measured by atomic clock B. Here 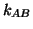 is a positive (``Doppler'')
factor whose magnitude expresses the motion of A relative to B. There are now
two time intervals: the one between the emitted pulses and the one
between the received pulses. These intervals are proportional to the
wavelengths of emitted and received monochromatic radiation. Their
ratio,
is a positive (``Doppler'')
factor whose magnitude expresses the motion of A relative to B. There are now
two time intervals: the one between the emitted pulses and the one
between the received pulses. These intervals are proportional to the
wavelengths of emitted and received monochromatic radiation. Their
ratio,
is the Doppler shift factor. The two radar units are
understood to be at rest relative to each other whenever 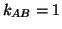 .
They are receding (resp. approaching) each other whenever
.
They are receding (resp. approaching) each other whenever 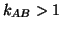 (resp.
(resp. 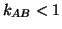 ), which expresses a Doppler red (resp. blue) shift. It is clear
that this Doppler shift of clock AB controls the rate at which the
back-and-forth bouncing pulse produces ticks at radar unit B. In fact,
the pulse arrival times of
), which expresses a Doppler red (resp. blue) shift. It is clear
that this Doppler shift of clock AB controls the rate at which the
back-and-forth bouncing pulse produces ticks at radar unit B. In fact,
the pulse arrival times of 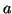 consecutive pulses coming from A are
consecutive pulses coming from A are
Similarly, the arrival times of 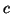 consecutive pulses coming from
radar unit C, which is part of clock BC, are
consecutive pulses coming from
radar unit C, which is part of clock BC, are
These two pulse sequences have coincident initial pulse arrival times
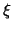 . If these two sequences are ``matched'', then their final pulse arrival times,
. If these two sequences are ``matched'', then their final pulse arrival times,
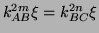 , also coincide. Under this circumstance the
length of these two pulse sequences as measured by atomic clock B are
the same. Consequently,
, also coincide. Under this circumstance the
length of these two pulse sequences as measured by atomic clock B are
the same. Consequently,
or
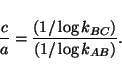 |
(5) |
This is the ticking rate of clock CB normalized relative to clock AB.
This ticking rate is a constant independent of the starting time 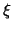 of the two matched pulse sequences. Consequently, clock AB is
commensurable with BC.
of the two matched pulse sequences. Consequently, clock AB is
commensurable with BC.



Next: Commensurable Accelerated Clocks
Up: Adjacent Clocks
Previous: Adjacent Clocks
Contents
Ulrich Gerlach
2003-02-25
![\includegraphics[scale=.5]{two_inertial_clocks}](img73.png)
![\includegraphics[scale=.5]{two_inertial_clocks}](img73.png)
![]() of two matched
pulse sequences impinging on radar unit B and coming from radar units
A and C? This ratio is determined by the following mini-calculation:
of two matched
pulse sequences impinging on radar unit B and coming from radar units
A and C? This ratio is determined by the following mini-calculation: