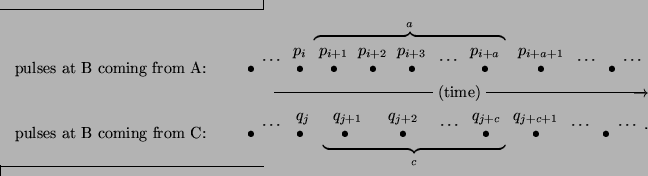
These sequences are depicted in Figures 5 and also in 6. We say that these two sequences are matched relative to B, and we write
To compare the operation of two adjacent geometrical clocks,
AB and BC one notes that they have radar unit B in common. Assume that all three
radar units A, B, and C move collinearly along the ![]() axis. The
common radar unit B has electromagnetic pulses bouncing off it.
There are those from A and those from C. Consider
axis. The
common radar unit B has electromagnetic pulses bouncing off it.
There are those from A and those from C. Consider ![]() consecutive pulses from A and
consecutive pulses from A and ![]() consecutive pulses from C:
consecutive pulses from C:

These sequences are depicted in Figures 5 and
also in 6. We say that these two sequences
are matched relative to B, and we write
The electromagnetic pulses impinging on B get partially reflected and
partially transmitted. Thus for every pulse sequence
![]() measured at B there are
corresponding sequences
measured at B there are
corresponding sequences
![]() and
and
![]() measured at A and C respectively.
Thus one has the following proposition (``Invariance of matched sequences''):
measured at A and C respectively.
Thus one has the following proposition (``Invariance of matched sequences''):
The property of being matched is invariant as each sequence of
pulses travels from one radar unit to another, i.e. if
As measured by atomic clock B, the ticking rates of geometrical clocks
AB and BC need not be uniform, and in general they are not. This is
evident from Figure 5. This deficiency is
remedied by calibrating the rate of pulses coming from C in terms of
AB. Thus for every ![]() -sequences of pulses departing from C and
arriving and counted at B, there is a matched
-sequences of pulses departing from C and
arriving and counted at B, there is a matched ![]() -sequence generated
by clock AB also at B. The ratio
-sequence generated
by clock AB also at B. The ratio
We say that the adjacent clocks AB and BC are normalizable if
both ratio (4) and ratio (5) are non-zero for every matched pair of ![]() and
and
![]() -sequences along the world lines of the two adjacent clocks. A
basic and obvious aspect of normalizability for adjacent clocks is
its reciprocal property: If AB is normalizable relative to BC, then BC is
normalizable relative to AB. Thus all collinear clocks AB, BC, BD, BE,
-sequences along the world lines of the two adjacent clocks. A
basic and obvious aspect of normalizability for adjacent clocks is
its reciprocal property: If AB is normalizable relative to BC, then BC is
normalizable relative to AB. Thus all collinear clocks AB, BC, BD, BE,
![]() , which share radar unit B, are mutually normalizable.
, which share radar unit B, are mutually normalizable.
Of particular utility are clocks which are commensurable. Their distinguishing property is obtained by subdividing the set of normalizable geometrical clocks further and selecting those whose normalized ticking rates, Eq.(4) or (5), are constant for all matched starting and termination pulses. Such clocks allow one to view the boost-invariant accelerated and the boost-invariant expanding inertial frames from a single perspective, which is developed in Section VII.
Before giving the precise general definition of commensurability (Section IV+.1667emB, we interrupt the developement by illustrating the above constellation of definitions, applying them to various combinations of inertial and accelerated clocks.
Nota bene: For the purpose of verbal shorthand we shall allow ourselves to refer to ``geometrical clocks'' simply as ``clocks''. However, for atomic clocks we shall use no such shorthand. Thus clocks without the adjective ``atomic'' are understood to be geometrical clocks, while atomic clocks are always referred to by means of the modifier ``atomic''.