


Next: Distant Clocks
Up: Adjacent Clocks
Previous: Commensurable Inertial Clocks
Contents
Again consider a pair of clocks AB and BC.
Figure 6:
Two adjacent geometrical
clocks consisting of collinearly accelerated cavities AB and BC,
each containing a pulse bouncing back and forth. Depicted in this
diagram is a sequence of 4 pulses coming from A and impinging on B
which are matched by a sequence of 8 pulses coming from C. The ratio
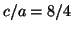 is the ticking rate of BC normalized to that of AB. The
fact that this ratio stays constant throughout the history of the
two clocks makes them also commensurable, just like those in
Figure 5
is the ticking rate of BC normalized to that of AB. The
fact that this ratio stays constant throughout the history of the
two clocks makes them also commensurable, just like those in
Figure 5
![\includegraphics[scale=.5]{two_accelerated_clocks}](img85.png) |
But this time have all
three of their radar units accelerate collinearly to the right with
respective constant accelerations 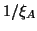 ,
, 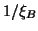 , and
, and 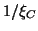 respectively, and with common future and past event horizons, as in Figure
6.
To make the discussion concrete, assume that
respectively, and with common future and past event horizons, as in Figure
6.
To make the discussion concrete, assume that
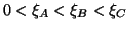 .
.
Consider the ticking produced by a pulse bouncing back and forth
in clock AB. The proper time between two successive ticks at A is
while at B it is
Their ratio
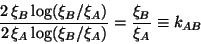 |
(6) |
is the pseudo-gravitational frequency shift factor. Similarly,
for clock BC one has
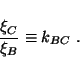 |
(7) |
These two frequency shift factors control the rate at which pulses arrive at
B from A and C respectively. In fact, the two corresponding matched pulse
sequences are
and
where the last pulse arrival time is the same, i.e.
or with the help of Eqs.(7) and (8)
 |
(8) |
This is the ticking rate of clock BC normalized relative to clock AB.
This ticking rate is a constant independent of the starting time
of the two matched pulse sequences. Consequently, accelerated clocks
AB and BC are also commensurable.

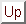


Next: Distant Clocks
Up: Adjacent Clocks
Previous: Commensurable Inertial Clocks
Contents
Ulrich Gerlach
2003-02-25
![\includegraphics[scale=.5]{two_accelerated_clocks}](img85.png)
![\includegraphics[scale=.5]{two_accelerated_clocks}](img85.png)