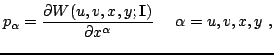


Next: Rotational Periodicity
Up: Action Variables
Previous: Linear Representation
Contents
2. Recalling that the four-momentum of the particle is
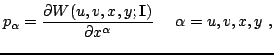 |
(52) |
one has the fact that these two sets of equations, (52) and (53), define implicitly the
phase space transformation
Being generated from the scalar function
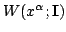 ,
this transformationis canonical, i.e. it leaves invariant the
representation of the antisymmetric tensor, Eq.(8):
,
this transformationis canonical, i.e. it leaves invariant the
representation of the antisymmetric tensor, Eq.(8):
Ulrich Gerlach
2005-11-07