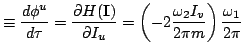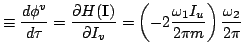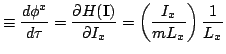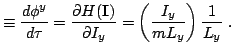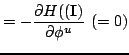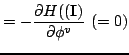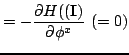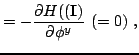


Next: Conclusion
Up: Action Variables
Previous: Rotational Periodicity
Contents
4. The evolution of a particle in the periodic electromagnetic field
of a travelling plane wave is mathematically equivalent to four
rotation processes. Together these processes, Eq.(![[*]](crossref.png) )-(51), describe a
point moving uniformly on a four dimensional torus. The four radii of
the torus are proportional to the action of four degrees of freedom
and their respective frequencies are
)-(51), describe a
point moving uniformly on a four dimensional torus. The four radii of
the torus are proportional to the action of four degrees of freedom
and their respective frequencies are
These equations will be recognized as the first half of Hamilton's equations
relative to action-angle variables.
The second half are simply
and they express what one knew all along, namely that the action
variables are constant along the particle path.



Next: Conclusion
Up: Action Variables
Previous: Rotational Periodicity
Contents
Ulrich Gerlach
2005-11-07
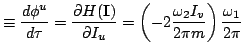
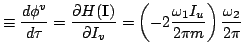
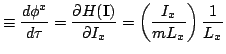
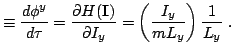
![[*]](crossref.png) )-(51), describe a
point moving uniformly on a four dimensional torus. The four radii of
the torus are proportional to the action of four degrees of freedom
and their respective frequencies are
)-(51), describe a
point moving uniformly on a four dimensional torus. The four radii of
the torus are proportional to the action of four degrees of freedom
and their respective frequencies are