


Next: MEASURING EVENTS VIA RADAR
Up: COMMENSURABILITY
Previous: Commensurable Accelerated Clocks
Contents
Distant Clocks
To compare the operation of two distant clocks, AB and CD,
note that they have four different radar units. Assume them to be moving
collinearly along the 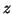 -axis such that A and D are the outer pair,
and B and C the inner pair, as in Figures 7 and 8
-axis such that A and D are the outer pair,
and B and C the inner pair, as in Figures 7 and 8
Figure 7:
Two distant
inertially expanding geometrical clocks. Clock CD can be calibrated
in terms of AB because CD and AB are commensurable: Taking into
account the ticking rate of the intermediate clock BC, one sees that
the ratio of their rates is a constant, namely 1:1. Because this
ratio happens to be unity, these two commensurable clocks are said
to have the additional property of being identically
constructed.
![\includegraphics[scale=.5]{two_distant_inertial_clocks}](img98.png) |
One says that two distant (nonadjacent) clocks AB and CD are
commensurable, or more briefly
if and only if
- (i)
- Radar units A and B are visible for all times to radar units C and D and
- (ii)
- AB is commensurable with BC, and BC is commensurable with CD.
Being ``visible'' means that, by using its pulse radar, C can always see B
on its radar screen, i.e. BC forms a geometrical clock.
Thus two clocks AB and CD are commensurable if the clock formed by
radar units B and C is commensurable with both of its neighbors, AB and
CD.
Figure 8:
Two distant
accelerated geometrical clocks. Clock CD can be calibrated in terms
of AB because CD and AB are commensurable: Taking into account the
ticking rate of the intermediate clock BC, one sees that the ratio
of their rates is
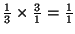 in this
figure. Because this ratio happens to be unity, these two
commensurable clocks are said to have the additional property of
being identically constructed.
in this
figure. Because this ratio happens to be unity, these two
commensurable clocks are said to have the additional property of
being identically constructed.
![\includegraphics[scale=.5]{two_distant_accelerated_clocks}](img100.png) |
According to this definition, one uses the constancy of the rate of clock CD
normalized to that of clock BC,
and the constancy of the rate of clock BC
normalized to that of clock AB,
to establish that the rate of clock CD
normalized to that of clock AB,
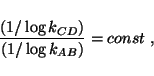 |
(9) |
is also a constant, and therefore that CD is commensurable with AB.
One sees from Eqs.(6) and
(9) that this criterion for
commensurability holds for both inertial and accelerated clocks, as is
depicted in Figures 7 and
8.
Commensurability of distant clocks subsumes that of adjacent clocks as
a special case. This follows from simply letting the space between
clocks AB and CD in Figures 7 and
8 shrink to zero so that the
final result is two adjacent clocks as in Figures 5 and 6. The
commensurability is readily preserved throughout this limiting
process.
Commensurability is a relation which satisfies the following three
properties![[*]](footnote.png) :
:
- AB
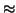 AB
AB
- AB
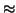 CD implies CD
CD implies CD 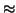 AB
AB
- AB
 CD together with CD
CD together with CD  EF implies AB
EF implies AB  EF
EF
A physicist can choose one of these commensurable clocks as his
primary standard. It is a dual function device : It represents a
temporal standard and a spatial standard at the same time. The
spatial extent of the clock is determined uniquely by its ticking
rate, a light pulse bouncing back and forth between the clock's two
ends.



Next: MEASURING EVENTS VIA RADAR
Up: COMMENSURABILITY
Previous: Commensurable Accelerated Clocks
Contents
Ulrich Gerlach
2003-02-25
![\includegraphics[scale=.5]{two_distant_inertial_clocks}](img98.png)
![\includegraphics[scale=.5]{two_distant_inertial_clocks}](img98.png)
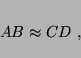
![\includegraphics[scale=.5]{two_distant_accelerated_clocks}](img100.png)
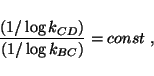
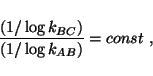
![[*]](footnote.png) :
: