There is, of course, the more common and familiar method. It does not use radar. Instead, it uses two distinct standards, namely, identically constructed clocks and standard rods Taylor and Wheeler (1992). The measuring procedure itself, we recall, consists of (i) locating the event by counting standard rods, and (ii) determining its time by counting at that location the ticks of the clock, which is synchronized to the standard clock.
One is now confronted with a question of consistency: Is this common non-radar method compatible with the radar method, even if the spacetime framework is based on inertially expanding or accelerated clocks?
Consider the common method of measuring an event. It consists of
starting with a geometrical clock having a spacetime history as depicted
in Figure 2 or
3. Such a clock is a standard
of time and of length. Thus a physicist forms a spatial array of
adjacent clocks AB, BC,![]() , EF,
, EF,![]() which are
identically constructed and synchronized. The definition is as follows:
which are
identically constructed and synchronized. The definition is as follows:
The ticking of adjacent clocks is synchronized by synchronizing the pulses impinging on their shared radar unit. This procedure guarantees synchronization of all clocks. It is exemplified in Figure 7. There the three clocks AB, BC, and CD have the phases of their internal pulses adjusted to tick in synchrony.
Suppose standard clock AB has its ![]() th (resp.
th (resp. ![]() st) ticking event
at its left (resp. right) radar unit A (resp. B). These events are
exhibited by Eq.(2) or
(3). Then, by induction, the left radar
unit of the
st) ticking event
at its left (resp. right) radar unit A (resp. B). These events are
exhibited by Eq.(2) or
(3). Then, by induction, the left radar
unit of the ![]() th identically constructed clock has its
th identically constructed clock has its ![]() th ticking
event at
th ticking
event at
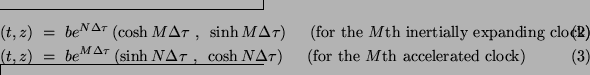
Having formed a linear array of such clock, the physicist uses the
lattice of events generated by their tick-tock actions as a standard
to measure an arbitrary event. The common method of measuring an event
consists of counting (i) how many clocks separate it from the standard
clock (![]() ), and (ii) how many clock ticks elapse before this event
happens. The result of these two counts is the pair of integers
), and (ii) how many clock ticks elapse before this event
happens. The result of these two counts is the pair of integers