MEASURING EVENTS VIA RADAR

Assume the physicist has chosen a standard clock whose cavity ends have relative frequency shift factor

$$k_{AB}\equiv e^{\Delta\tau}~.$$

This Fourier compatibility factor controls the clock rate, which in turn controls the times that outgoing pulses leave the clock and the times that the receiver is turned on to allow the reception and recording of incoming pulses.

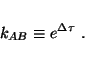
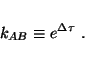
Events have a commensurable property, a property which is reducible (by a process of counting) to a standard of length and of time. The common method of measuring events, and historically the first, relies on counting replicas of a standard of length and synchronized replicas of a standard of time in order to identify an event in terms of coordinates. The standard of length and of time were considered distinct and independent of each other. But Einstein, by a process of hard work, noticed that (i) it takes an act of using ones visual faculties, and hence a familiarity with the properties of light, and that (ii) one must have a clear understanding of what is meant by ``looking at clocks which are synchronized'', before one can claim to have measured an event.

With that observation it became clear that the standard of length and the standard of time cannot be chosen independently, but are related by the speed of light.

Suppose radar had been invented before 1905. Then using the method of radar to measure events would have forced a physicist to confront and solve the problem of using synchronized clocks before 1905. He would have immediately found from his observations that the standard of length is related to the standard of time. Further more, by following Bondi Trautman et al. (1965), the physicist would have immediately formulated the kinematics of special relativity, saving himself the hard work that Einstein had to do.

Both the method of radar and the common method for measuring an event have been formulated for radar sets, clocks, and measuring rods which are unaccelerated and static relative to one another. Can one extend these two formulations and will they remain equivalent if on drops these restrictions? The following sections give an affirmative answer.