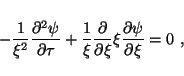
The complementary, but equivalent (via Fourier synthesis), perspective
on this resonance is to note that the two clocks have identical normal
mode spectra. More explicitly, the cavities have their ends moving in
such a way that the normal modes, which are governed by the wave
equation
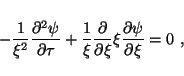
For the circumstance of two inertially expanding clock cavities AB and CD
this is achieved by the condition
![[*]](footnote.png)
The results expressed by Eqs.(24) and (26) can therefore be summarized by the simple statement:
Identically constructed clocks are those with cavities having
identical eigenvalue spectra.
This means that the frequencies![[*]](footnote.png) of the field oscillators in one cavity coincide with the frequencies
of those in the other.
of the field oscillators in one cavity coincide with the frequencies
of those in the other.
If there is a weak mutual interaction between the cavities (i.e. the reflectors at the cavity ends are slightly transmissive), then there is a coupling among each pair of normal modes (field oscillators), one in each of the two cavities. If cavity AB starts out with all the field energy, then this coupling mediates the excitation of the field oscillators in CD at their respective frequencies. They will start oscillating in sympathy with those of AB.
The sum of all the (normal mode) amplitudes of these field oscillators forms a bouncing pulse in CD. The fact that the sympathetic resonance makes these amplitudes increase with time implies that the bouncing pulse in CD does the same.
To summarize: An analysis in terms of bouncing pulses or in terms of normal modes leads to the same conclusion: The physical process of the transfer of time (a train of clock ticks) between identically constructed clocks is the process of sympathetic resonance between their cavities.