


Next: TRANSFER OF RADAR DATA
Up: RADIATION FROM BODIES WITH
Previous: Normal Modes
Contents
TRANSFER OF TIME ACROSS FROM AN ACCELERATED TO AN INERTIALLY EXPANDING
CLOCK
Figure 11:
One-way
commensurability between inertially expanding clock AB and
accelerated clock BC, each containing its pulse bouncing back and
forth. Depicted in this diagram is a sequence of 5 high intensity
pulses coming from A and impinging on B which are matched by a
sequence of 4 low intensity pulses coming across the event horizon
from C. The ratio 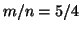 is the ticking rate of AB normalized to
that of CD. The fact that this ratio stays constant throughout the
history of the two clocks makes them one-way commensurable.
is the ticking rate of AB normalized to
that of CD. The fact that this ratio stays constant throughout the
history of the two clocks makes them one-way commensurable.
![\includegraphics[scale=.5]{accelerated_and_inertial_clocks}](img149.png) |
Commensurability is a more basic property than the property of clocks
being synchronized. Before one tries to synchronize two clocks,
one must first ascertain that they are commensurable.
Furthermore, two commensurable clocks cannot be synchronized unless there is a
two-way interaction between them. In the context of an inertially
expanding or an accelerated coordinate frame (Figure 9 or 10) such an
interaction consists of a radar (to and fro) signal between each pair
of clocks, say AB and CD as in Figures 7 or 8. Such a radar
signal accommodates a two-way transfer of time: AB transmits its tick
number to CD, and CD sends via the return pulse its own tick number
back to AB. With this mutual knowledge the two clocks can be
relabelled, if necessary, to give synchronized time.
However, if there is an event horizon between clocks AB and CD, then
qualitatively new considerations enter.
On one hand, at most only a one-way transfer of time is possible. The
establishment of a time synchronous to both of them is out of the
question.
On the other hand, that event horizon brings with it a pleasant
surprise: an accelerated clock and an inertially expanding clock,
which at first sight seem to be incommensurable, are in fact
commensurable when there is an event horizon between them. In
particular one clock can (via sympathetic resonance) exert a one-way
control over the other. Here is why:
As one can see from Figure 1 there is an
event horizon that separates the clocks in spacetime sector 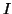 from
those in spacetime sector
from
those in spacetime sector 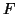 . But the problem with taking advantage of
a one-way transfer of time from CD in
. But the problem with taking advantage of
a one-way transfer of time from CD in 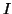 to AB in
to AB in 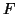 seems to be
that the clock in
seems to be
that the clock in 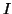 is accelerated while the one in
is accelerated while the one in 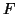 is
inertially expanding. At first sight there seems to be no way that the
two are commensurable as defined on page
is
inertially expanding. At first sight there seems to be no way that the
two are commensurable as defined on page ![[*]](crossref.png) in
section IV+.1667emB. One must note, however, that that
definition was based on a two-way transfer of time (``AB is
radar-visible to CD''). This was necessary. Indeed, the definition of
boost-invariant sector
in
section IV+.1667emB. One must note, however, that that
definition was based on a two-way transfer of time (``AB is
radar-visible to CD''). This was necessary. Indeed, the definition of
boost-invariant sector 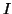 as well as
as well as 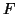 (``equivalence classes of
geometrical clocks that can be synchronized'') depended on it.
(``equivalence classes of
geometrical clocks that can be synchronized'') depended on it.
To accommodate the context of an event horizon as a one-way membrane
between clocks AB and CD, we enlarge the concept ``commensurability''
by defining the concept ``one-way commensurability''. This is done by
dropping the requirement that radar units B and C be in two-way
contact, and by saying that one-way contact, say from C to B,
is good enough. The result of doing this is
illustrated in Figure 11.
Accelerated clock CD moves along the line of sight of inertially
expanding clock AB. This clock is characterized by Doppler shift
factor 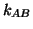 .
Clock CD, whose radar units are accelerated with constant
accelerations
.
Clock CD, whose radar units are accelerated with constant
accelerations 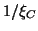 and
and 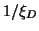 to the right, is
characterized by the pseudo-gravitational frequency shift factor
to the right, is
characterized by the pseudo-gravitational frequency shift factor
between them. As shown in Figure 11, clock CD sends pulses on a one-way journey to AB. There are
no return pulses. Nevertheless, one can compare a sequence of 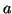 pulses at B from A with a matched sequence of
pulses at B from A with a matched sequence of  pulses from CD.
The result is
pulses from CD.
The result is
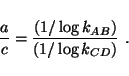 |
(24) |
This is the ticking rate of inertial clock AB normalized relative to
accelerated clock CD. This ticking rate is a
constant independent of the starting time of the two matched pulse
sequences. Consequently, inertial clock AB is one-way
commensurable with accelerated clock BC.
Figure 12:
One-way transfer of time from
clock CD to clock AB. This transfer is achieved by the ticking of CD
causing sympathetic tickings in clock AB. This process is brought
about by e.m. pulses travelling from CD across the future event
horizon to AB (solid thin 45 lines). They strike B at
precisely the same rate and with the same phase as AB's clock pulse
(heavy zigzag line) bouncing repeatedly off B.
lines). They strike B at
precisely the same rate and with the same phase as AB's clock pulse
(heavy zigzag line) bouncing repeatedly off B.
![\includegraphics[scale=.6]{resonating_clocks_inF_and_inI}](img153.png) |
Equation (27) is a remarkable
result for a number of reasons. First of all, there is its
constancy. Contrast this with the tickings of the comoving atomic clocks
at radar units B, which is floating freely, and C, which is
accelerated. They yield
a corresponding rate which is a
Doppler chirp towards the red as seen by a physicist comoving with the
free-float atomic clock at B. By contrast, the constancy of
Eq.(27) expresses the fact that
the slowdown in the proper
ticking rate of geometrical clock AB compensates precisely for the
slowdown in the proper rate of pulses arriving at B from C.
Second, if 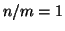 , i.e.
, i.e.
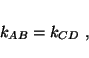 |
(25) |
then the process of transferring a train of clock pulses from across
its future event horizon to clock AB (``one way transfer of time'') is
a process of tickings in cavity CD bringing about sympathetic tickings
in cavity AB. The implementation of this transfer is depicted in
Figure 12. Thus, following the discussion in
Section VI, one concludes that,
even though CD is accelerated while AB is expanding inertially, (i)
the two cavities are identically constructed from perspective
of their normal mode spectra, and that (ii) AB and CD are
ticking at the same rate as measured at B.



Next: TRANSFER OF RADAR DATA
Up: RADIATION FROM BODIES WITH
Previous: Normal Modes
Contents
Ulrich Gerlach
2003-02-25
![\includegraphics[scale=.5]{accelerated_and_inertial_clocks}](img149.png)
![\includegraphics[scale=.5]{accelerated_and_inertial_clocks}](img149.png)
![]() from
those in spacetime sector
from
those in spacetime sector ![]() . But the problem with taking advantage of
a one-way transfer of time from CD in
. But the problem with taking advantage of
a one-way transfer of time from CD in ![]() to AB in
to AB in ![]() seems to be
that the clock in
seems to be
that the clock in ![]() is accelerated while the one in
is accelerated while the one in ![]() is
inertially expanding. At first sight there seems to be no way that the
two are commensurable as defined on page
is
inertially expanding. At first sight there seems to be no way that the
two are commensurable as defined on page ![[*]](crossref.png) in
section IV+.1667emB. One must note, however, that that
definition was based on a two-way transfer of time (``AB is
radar-visible to CD''). This was necessary. Indeed, the definition of
boost-invariant sector
in
section IV+.1667emB. One must note, however, that that
definition was based on a two-way transfer of time (``AB is
radar-visible to CD''). This was necessary. Indeed, the definition of
boost-invariant sector ![]() as well as
as well as ![]() (``equivalence classes of
geometrical clocks that can be synchronized'') depended on it.
(``equivalence classes of
geometrical clocks that can be synchronized'') depended on it.
![]() .
Clock CD, whose radar units are accelerated with constant
accelerations
.
Clock CD, whose radar units are accelerated with constant
accelerations ![]() and
and ![]() to the right, is
characterized by the pseudo-gravitational frequency shift factor
to the right, is
characterized by the pseudo-gravitational frequency shift factor
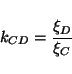
![\includegraphics[scale=.6]{resonating_clocks_inF_and_inI}](img153.png)
![]() , i.e.
, i.e.