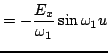 |
(30) | |
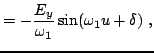 |
(31) |
In mechanics, periodicity, one of the most pervasive aspects of nature, leads to the introduction of action-angle variables as phase space coordinates for a dynamical system. One of the chief virtues of these variables is that they decompose the given dynamical system into its fundamental components, a set of noninteracting subsystems (``degrees of freedom'') each having its own frequency. This is why some mathematicians2, call these coordinates ``normal coordinates'', in analogy with the normal modes of a linear vibrating system.
Suppose the charged particle moves in the periodic electromagnetic field of a plane wave
| (32) |