The consistent use of geometrical clocks puts constraints on the
mathematical formulation of waves propagating in the inertially
expanding coordinate frame ![]() . In this frame, a standard inertially
expanding clock AB characterized by Doppler frequency shift factor
Eq.(25),
. In this frame, a standard inertially
expanding clock AB characterized by Doppler frequency shift factor
Eq.(25),
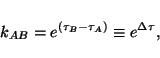
| (26) | |||
| (27) |
In a paper some time ago Padmanabhan (1990) Padmanabhan
considered the evolution of normal modes of the wave equation
![]() in the boot-invariant coordinate frame
in the boot-invariant coordinate frame ![]() .
.
Starting with a normal mode characterized by positive boost
frequency in the distant past of ![]() , he observed that this mode, in
compliance with the wave equation, evolved into a mixture of positive
and negative frequencies in the distant future of
, he observed that this mode, in
compliance with the wave equation, evolved into a mixture of positive
and negative frequencies in the distant future of ![]() . From the
viewpoint of quantum theory such a mixture indicates a production of
particles and antiparticles. This formulation of waves propagating in
. From the
viewpoint of quantum theory such a mixture indicates a production of
particles and antiparticles. This formulation of waves propagating in
![]() therefore leads to the mathematical prediction that, in analogy
with Parker's particle-antiparticle creation mechanism
Parker (1982) due to a time-dependent gravitational field,
particles and antiparticles get created because of the time-dependence
of the boost-invariant metric, Eq.(33), in
therefore leads to the mathematical prediction that, in analogy
with Parker's particle-antiparticle creation mechanism
Parker (1982) due to a time-dependent gravitational field,
particles and antiparticles get created because of the time-dependence
of the boost-invariant metric, Eq.(33), in ![]() .
.
This prediction is, of course, invalid. It contradicts the absence of any such particle creation in flat spacetime, where there is no gravitational field. But the procedure leading to this contradiction, Padmanbhan points out, is mathematically sound and completely conventional [our emphasis]. In order to avoid this contradiction he proposes that, within the context of quantum theory (i.e. particle-antiparticle production), one exclude Bondi and Rindler's spacetime coordinatization as physically inadmissible.
However happy one must be about the scrutiny to which that coordinatization has been subjected, one must not forget that Padmanabhan's procedure leading to to the above contradiction is far from ``completely conventional''. In fact, it violates the central principle of measurement (Section III): ``once a standard of time has been chosen, it becomes immutable for all subsequent measurements''. Here is how the violation occurs:
In spacetime sector ![]() , where the invariant interval has the form
, where the invariant interval has the form
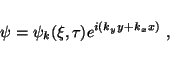
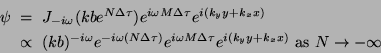
Note that even though this clock-controlled sampling measurement
reconstructs the the field uniquely in the distant past (![]() ) of
) of ![]() , it is clear that this is not the case in the distant
future (
, it is clear that this is not the case in the distant
future (![]() ). Regardless how small one makes the separation
between the sampling events in the asymptotic past, in the asymptotic
future the inertially expanding clocks tick at such a slow rate (compared
to any atomic clock) that there is no possibility of reconstructing
the field from the sampling measurements. Indeed, in the distant
future (
). Regardless how small one makes the separation
between the sampling events in the asymptotic past, in the asymptotic
future the inertially expanding clocks tick at such a slow rate (compared
to any atomic clock) that there is no possibility of reconstructing
the field from the sampling measurements. Indeed, in the distant
future (
![]() ), the field,
Eq.(35),
), the field,
Eq.(35),
![\begin{eqnarray*}
\psi\approx\frac{1}{2}\sqrt{\frac{2}{\pi k\xi}}
&~&\!\!\!\!\!\...
...\pi/4)}
\right]
\\
&~&\times ~e^{i\omega \tau}e^{i(k_yy+k_x x)}
\end{eqnarray*}](img187.png)
Would an atomic clock do better? The answer is yes. But only for
sampling measurements made in the distant future
(
![]() ). For the distant past
(
). For the distant past
(
![]() ) atomic clocks are just as useless
as inertially expanding clocks are for the distant future: the clocks
simply do not sample the field fast enough to identify its boost
oscillation frequency.
) atomic clocks are just as useless
as inertially expanding clocks are for the distant future: the clocks
simply do not sample the field fast enough to identify its boost
oscillation frequency.
Thus neither atomic clocks nor inertially expanding clocks can give
measurements which identify the nature of the field in both the
asymptotic past and the asymptotic future of ![]() . One can measure the
field in one or the other but not both.
. One can measure the
field in one or the other but not both.
A claim that in boost-invariant sector ![]() a pure positive boost
frequency (
a pure positive boost
frequency (![]() ) mode evolves into a superposition of positive and
negative inertial frequency (
) mode evolves into a superposition of positive and
negative inertial frequency (![]() ) modes is wrong. This is because
it makes the tacit assumption that one change inertially expanding to
static atomic clocks in midstream. Making such a change would go
counter to the central principle of measurement (Section
III): ``once a standard has been
chosen it becomes immutable for all subsequent
measurements''. Violating it would make a standard into a
non-standard.
) modes is wrong. This is because
it makes the tacit assumption that one change inertially expanding to
static atomic clocks in midstream. Making such a change would go
counter to the central principle of measurement (Section
III): ``once a standard has been
chosen it becomes immutable for all subsequent
measurements''. Violating it would make a standard into a
non-standard.
But a standard is precisely what is needed, otherwise there would be no way of assigning a frequency and a direction of propagation to normal modes, the key ingredients to mode amplification and hence to particle creation as formulated in quantum field theory. Put differently, an assertion that a mode having a positive frequency evolve mathematically into a mixture of positive and negative frequency modes must be accompanied by a specification of a (system of commensurable) standard clock(s).
It is evident that in sector ![]() no such standard exists.
Consequently, one is not entitled to claim that mathematical analysis
of free fields in that sector predicts the creation of particles.
no such standard exists.
Consequently, one is not entitled to claim that mathematical analysis
of free fields in that sector predicts the creation of particles.